Design of Experiments (DOE) – An essential tool to better understand tablet formulations

This paper covers a brief overview of the steps for pharmaceutical product development under the quality by design (QbD) framework; introduces design of experiments (DoE) applied to formulation of tablets and gives an example of how to design piroxicam amorphous solid dispersions (ASD) tablets using DoE.
Steps for product development
A successful product development effort should include 3 main steps: planning, controlling, and improving. The planning phase includes gathering all product requirements and performing risk analysis to identify critical quality attributes of the product; we call this the “Quality Target Product Profile” (QTPP) document. This is primarily a summary of the drug product characteristics that ideally will be achieved to ensure the desired quality, safety and efficacy for the patient.

under the QbD framework.
The second step starts with understanding product and process design to develop control strategies (CS) for the development and manufacture processes.
It is only when product and process are understood that improvements through the product life cycle can be suggested.
All these 3 stages sound obvious and are no more than applying good science and common sense. There are tools that facilitate the successful implementation of the 3 steps described in Figure 1.
Risk assessment (RA) and DoE are becoming a must not a desirable tool in product development. Critical materials attributes (CMAs) factors, critical process parameter (CPPs) factors and critical quality attributes (CQAs) responses must be identified, so an effective and meaningful experimentation can be designed.
Design of Experiments
When formulating tablets, it is quite possible that at least 3 critical factors would need to be investigated because they
might impact the responses (CQAs) measured. For this example, the 3 factors are: amount of disintegrant (Ac-Di-Sol®), diluent (Pearlitol® SD 200) and binder (Avicel PH102) in the formulation. If, e.g., 5 levels (conditions) are investigated per factor, 125 experiments [(5 levels)3factors = 5x5x5 = 125] would have to be performed to cover all possible formulation conditions. This is not a very efficient way to find out the effects of changing these 3 factors on CQAs (responses) of the product, e.g., tensile strength, solid fraction, disintegration time and friability.
A better way is to have experiments with a controlled set of tests designed to model and explore the relationship
between factors and one or more responses. For formulation development, mixture design is recommended. In a
mixture experiment, the factors are proportions of different components of a blend.
Amorphous solid dispersion tablet formulation using DoE tools
Table 1 shows the example used in this paper. When the mixture components are subject to the constraint that they must sum to a fixed amount, in this case 68.25%, there are standard mixture designs for fitting models, e.g., simplex, lattice, simplex centroid, reduced simplex-centroid and extreme vertex [1].
The first step is to create the design by defining the responses (CQAs) and factors (CMAs); specifying the model; generating the design and making the table (Figure 2).
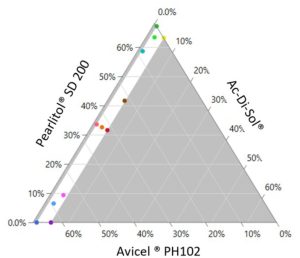
18 randomised experiments have been generated. For each formulation condition (runs 1-18), tablets have been produced using the STYL’One Nano (MEDELPHARM, FR) instrumented tablet press. The experiment set up and tablet compression were controlled by the Alix software (MEDELPHARM, FR).
Once the experiments are performed and the responses measured, the data analysis includes visualising the data (Figure 3); fitting the model (Figure 4); analysing variance (Table 2); plotting prediction profiler (Figure 5) and analysing the contour profiler (Figure 6).
Visualising the data is a powerful tool. It might indicate which are the main factors for each response or if there are outliers to be investigated. Plotting all responses across all factor’s ranges can show main trends of the dataset.

Figure 3 shows the plots for each response as a function of the factors studied. Each datapoint shows one response value (Y axis) at each factor level (X axis), while the smooth line depicts the overall trend.
For example, the lines indicated that an increase in the proportion of Avicel® PH102 resulted in a gain of solid fraction and tensile strength, but a decrease in ejection pressure and friability. The lines show opposite trends for Avicel® PH102 and Pearlitol® due to the mixture design, because each component compensates each other proportion to a fixed amount. On the other hand, the responses datapoints as a function of the disintegrant % are spread over the experimental range, resulting in lines without a trend. The lack of relationship between the Ac-Di-Sol® and responses values can be assigned to the narrow variation of this components is this mixture design (1-5 %).
Fitting the model requires the compilation of statistical tests. In this step, variation of the data and how it might affect the hypothesis on the relationship between factors and responses are evaluated. This step might also include comparing different models to check which ones better fit the data.
To begin, the model terms are selected, e.g., main factors and second factor interactions. For this example, there are 3 main terms (Avicel® PH102, Pearlitol® SD 200 and Ac-Di-Sol®) and 3 interaction terms (Avicel® PH102xPearlitol® SD 200, Avicel® PH102xAc-Di-Sol® and Pearlitol® SD 200xAc-Di-Sol®).
The actual by predicted plot (Figure 4) shows the model trend line for tensile strength (Figure 4A) and friability (Figure 4B) in red and the experimental response values and the response value for each datapoint (18 runs). From the plot it can be observed that, for the response tensile strength the model fitted the data well. It also shows how consistent the results are including the repeats. For a good fit, the points should be close to the fitted line, with narrow confidence bands. The actual by predicted plot for friability indicates a good fit, but a wider confidence interval means this estimate is expected to have larger variation range around the predicted friability value.
The analysis of variance (Table 2) includes the R2Adjusted value which represents the proportion of the dataset variation explained by the model, and the closer to 1 the better; the F-Ratio represents the responses signal-to-noise ratio, the higher the better; the p-value is the output of the statistical test, and confirms that the effect is significant, not a result of random chance.
The smaller the p-value the more likely the term is to be a real effect. For p-value below 0.05 the, the factors are statistically significant.
Figure 5 shows the prediction profiler for the responses and factors studied.
It provides a dynamic way to see how predictive model changes as the settings of individual factors change.
Desirability goals can be set for the responses to find optimal settings for the factors.
For example, if the goals are for tensile strength 2.10 MPA, solid fraction 0.81, disintegration time 159 s and friability 0.29%, the factors should be set to Avicel PH102 36.9%, 28.6 % Pearlitol® SD 200 and Ac-Di-Sol 2.69% as described in Figure 5.
Characterisation of Avicel® PH102 revealed that this excipient plastically deforms at low compression pressure and form bonds between its particles. Interparticle bonding increased the strength of the tablet [2]. The predicted solid fraction plot, despite the narrow range values (0.785 – 0.815), shows that as you increase the Avicel® PH102 %, the solid fraction increases, therefore increasing the density of the tablets produced at the same pressure (120 MPa).

The effect of Avicel® PH102 in solid fraction can be explained by differences in Avicel® PH102 – Pearlitol® 200 SD compaction mechanism.
Avicel® PH102 is a soft-ductile material, while Pearlitol® 200 SD is moderately hard-ductile [3].
Therefore, Avicel® PH102 will deform at lower forces than Pearlitol® 200 SD. As the compression pressure selected to run the formulation experiments was relatively low (120 MPa), the proportion of Avicel® PH102 contributed the most to the increase of solid fraction.
Figure 6 shows the contour profiler based on the ranges and goals described above.
The grey area is restricted by the design constrains; the shady areas blue and red are restricted by responses upper and lower limits and the white shows the ‘design space’ (DS)where the conditions are expected to produce formulations that meet the QTPP specifications.
See the full brochure Design of Experiments (DOE) here:
(click the picture to download the brochure)
Source: MEDELPHARM brochure Design of Experiments (DOE)
Maybe you can take part in the MEDELPHARM university contest – Have a look!






